All our products made in U.S.A.
""
Your student should start by simply trying to make the Bead Patterns shown.
This activity builds a familiarity with the components of Mac's Abacus, and how they move.
Some of these patterns are simply aesthetic. But others (A, B, C, D, E, M, N, O & P) draw a subtitle attention to counts, as your student arranges the Beads into Groups of 2, 3, 4, 5, 9 & 10.
A great place to start ...Kids really love this part!
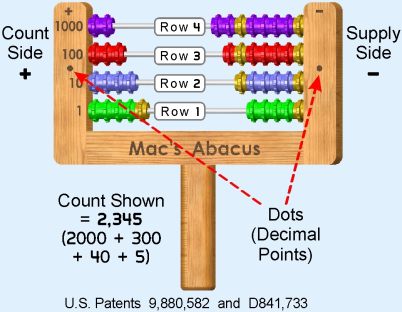
Counting begins by simply matching loose Beads to same-color Beads of the Abacus Rows. Special Tape-on Legends assign the count-objects to specific Bead Rows.
The use of each Bead Row as an individual Counter allows for a side-by-side comparison of four Counts. These comparisons help to build the notion of Quantity (greater-than, equal-to, less-than) in your student's mind, thus working to form a solid visual/conceptual understanding of Value …Size …Magnitude.
The first half of the workbook uses these Legends to make comparisons that expand on the concepts.
Counting now moves to matching each Abacus Bead to other objects, as indicated in the Legend (Hearts, Stars, Cheerios™ and Balls). This conceptual move from matching Beads <=> Beads to matching Objects <=> Beads is what allows us to use Numbers to represent and thus to manipulate the things in our world.
Notice the Consistency of Counts, as two objects always = 2 Beads and
three objects always = 3 Beads (also demonstrated in Lesson 1).
The objects are clustered into groups of 2, 3, and 4 as a subtle encouragement for your student to select the Beads in corresponding groups. (After having already done many Lessons, there will be a natural tendency toward the “efficiency” of moving more than one Bead at a time).
Developing the ability to visualize Groups is a fundamental skill that leads to the understanding of many practical groupings such as: [by 2's, 5's, 10's, 100's, Dimes, Dollars ...].
Playing cards are used to connect the Numerical Digits with the actual Group Counts. At this point, your student is encouraged to Print the corresponding digits on the lines next to the Abacus Rows. This presents a 3-way direct correspondence:
(the Count of Objects <=> the Count of Beads <=> the Printed Number.)
Your student can learn to print the numbers by using the Practice Sheet at the back of Mac's Abacus Basic Workbook.
Now your student counts on his/her fingers, which forms a direct correspondence between the Number of Fingers, the Number of Beads on that Abacus Row and the Numerical Digit assigned to that Count, thus deepening and personalizing your student's understanding of Quantity …Value …Magnitude.
The complete set of Finger Counts is also shown in the First Counts Poster on the back of Mac's Abacus Basic Workbook
Now that Counts of “real” objects has become understood, the Concept of Zero is presented. After having counted the parts used to make prior toys, some toys are shown that do not use one of the listed parts. Therefore, no Purple Connectors are used here (so their Count = 0 ).
Many following Math Lessons in our Workbook present the Concept of Zero in different ways.
The Concept of Zero is presented here by using a “blank” Die (one with no Dots!) in the set of Dice.
For a different presentation of The Concept of Zero, see the Subtraction Poster, on the inside back cover of your Mac's Abacus Basic workbook.
“Formal Addition” is subtly introduced by presenting the “+” symbol between pairs of Dice.
Since these pairs are already within a colored circle, it is already obvious that the Count is the total count of dots encircled.
Also, the “=” sign is presented, shown to be pointing to the “Equivalent” Bead Row.
With frequent use in the Lessons that follow, the meaning of “+” and “=” becomes intuitively obvious to your student.
The “+” and “=” signs become more prominent as they are used to combine the counts of two or three Cards. Thus the process of Addition and the forming of written equations is demonstrated.
Using Cards is an example of how we present Early Math Concepts as being very useful as well as Fun!
Now that familiarity with printed Numbers and with the “+” and “=” signs has been established, Counting is presented in the purely abstract form ( 4 + 1 = 5 ).
The use of four Problems (one on each of the four Bead Rows) provides the direct comparisons that confirm the consistency of these Counts. It becomes easy to see how these parts come together.
Now that Counts and their meaning as size and quantity have been understood, this notion of “size” is shifted to represent Lengths.
Here, various sized Rods are stacked end-to-end. Their size is defined by their colors, which is shown in the Key at the upper right of the Lesson. Below each of the four problems are the sizes printed as Numbers and “stacked together” by the connecting “+” signs. Their Total Length is called for by the “=” sign.
Having four Problems together on Mac's Abacus Bead Rows gives your student the visual confirmation that “Lengths” add up consistently as have all the previous Counts.
Another quantity “Time” is presented by focusing just on the Hours of clocks as units of Count. In this Lesson, the equivalence of the Hour Number, its correspondence to the Bead Count and to the Printed Number are further used to verify the equivalence of both Dial and Digital clocks.
The Concept of “Subtraction” is shown as a Removing of Counts. Here, your student starts with the Counts of the now familiar Lesson 96 (shown in the Key at the upper right of this Lesson).
Then any “X'ed out” Counts are subtracted from the previous total by simply moving Beads from the + side of the Abacus to the - side (notice the + and - markings on the sides of Mac's Abacus.
For clarity of action, the Beads in each Row are shown grouped as they occur on the dice ...this technique is used extensively in the answers of our Teaching Guide.
As was done with Addition, Subtraction is presented in the purely abstract form ( 5 + 1 - 2 = 5 ). Your student starts with the Counts of the now familiar Lesson 116 (shown in the Key at the upper right of this Lesson). Then the value of the “- Digit” is subtracted from the previous total by simply moving that many Beads from the + side of the Abacus to the - side.
By starting with values established in a previous “Addition” Lesson (116), this new experience proceeds from a position of familiarity, thus inspiring confidence in the process.
The now familiar Group Count is expanded upon by assigning a “Token” to represent a specific quantity of a specific item (here 1 Token = 2 Basketballs). Your student is to count “2 Basketballs” at each occurrence of this Token. This means the Token is worth 2 Beads on the associated Bead Row.
The concept of a Token is the next level of abstraction after Groups. As will be soon demonstrated, it leads to such concepts as Money and the structure of our Decimal System (Place Value).
Here, the Nickel becomes the Token and its value is (conveniently) set = 5 Pennies. This Lesson expands your student's horizon by showing that a Token may have other appearances and may also be assigned to represent other objects.
The fact that this particular assignment is “true” in the real world is a subtle prelude to the later introduction of Money in Mac's Abacus Basic workbook.
Here the (Blue) Bead of Row 2 is designated as a Token whose value is set = all 10 Beads of Row 1.
For the first time in our Workbook, the Tape-On Legend is removed, so the first 2 Bead Rows may be used to efficiently hold Counts greater than 10 ! The assignment of this Token is shown in the Key (top corner). The numerical equivalent of this Lesson is shown printed in “Standard Form” on lines to the left of the Abacus.
Your student is encouraged to print the results in the Standard Form, based on the Counts of Beads in the associated Abacus Rows.
The total count of loose parts exceeds 10, so as we count them, we will run out of Beads in Row 1.
Remember that the token Blue Beads in Row 2 are assigned the value of all 10 Beads of Row 1, which allows us to “Trade” all 10 Beads of Row 1 for 1 Blue Bead (as shown in the inset). That done (also called a Carry), we can continue counting the loose parts to arrive at the total (=12).
This Trade (Place Value) is the fundamental structure of our Decimal System! (During a Subtraction, we Trade in the other direction as needed, calling it a “Borrow”)
Using the Beads of Row 2 as a Token, whose value equals all 10 Beads (green) of Row 1, allows Counting to progress all the way through the “90's”.
Here, Dice are counted, starting on Row 1.
When the Count reaches 10 (=10 Beads), these 10 Beads of Row 1 are “Traded” for one Bead (Blue) on Row 2. (i.e. All the 10 Beads of Row 1 are reset to the Supply Side (-) and 1 Blue Bead is moved to the + side).
Since this cluster of Dice = 22, there will be two “trades” ( a [5+5, trade], a [5+4+1, trade], then [+ 2] = 22 ).
Now the Red Bead of Row 3 is defined as a Token, whose value equals all 10 Beads (Blue) of Row 2.
Thus, one Red Bead = 10 x 10 = 100, so Row 3 can hold Counts into the “900's”.
Here, the Numbers to Add are scattered about.
Once your student has added them all, he/she should print the total (based on the Beads counted in the Abacus Rows) in the box as shown.
Notice that the Place Value of both Tokens (Red and Blue Beads) are defined in the Key.
It is now assumed that the Blue and Red Beads are both assigned the value of all 10 Beads in the next-lower Row.
The Money Tokens for the Coins (Nickel, Dime and Quarter) are defined in terms of Pennies (in the Key). Using these assignments, the array of scattered coins is counted as (25 + 25 + 25 + 10 + 10 + 5 = 100). Since the “token” assignments are the values of real coins, your student is learning to Count Money by using our Decimal System!
Notice the DOTS branded into both sides of Mac's Abacus between Rows 2 and 3. These can be interpreted as separating the Dollars from the Cents!
Paper Money (having been introduced in prior Example Lessons) is presented, along with an assortment of Coins.
The Purple Bead of Row 4 is defined as a Token, whose value equals all 10 Beads (Red) of Row 3. Thus, 1 Purple Bead = 10 x 100 = 1000 (= $10.00), so Row 4 can hold Counts through the $90.00's. Once all the Money is Counted, your student should print the results on the lines provided, based on the counts of Beads in the associated Abacus Rows. He/she should include the “Decimal Point” as it occurs between the Red and Blue Bead Rows.
The last Lessons of Mac's Abacus Basic Workbook demonstrate the ability of your student to not only Count and to Add and Subtract large numbers, but also to recognize Money and to use these skills to “buy” items with Money from an “allowance” (as given in the Key) and to compute the change!
Your student now has a fairly deep understanding of Addition, Subtraction, our Decimal System and our Monetary System.
Furthermore, he/she has an intuitive feel for some magnitudes of quantities and has developed a practical application for Math.
Our 5-STAR Collection
© 2023 LearnTools Inc.